معروف عن مساحة المثلث على انها نصف القاعدة مضروبة في الارتفاع. هذا القانون سيكون ساري لو كانت هناك زاوية قائمة في المثلث ومعروف طول ضلعيه العمودي والأفقي. ايجاد الضلع الثالث سوف نطبق قانون الوتر والذي يساوي جذر مجموع مربعي الضلعين العمودي والأفقي. كل هذا سيكون سهل وبسيط في أي مثلث قائم الزاوية. ولكن ماذا لو كان المثلث غير قائم الزاوية هل يمكن تطبيق هذه القوانين عليه. زيادة على ذلك كيف يمكن إيجاد أطوال أضلاع المثلثات غير قائمة الزاوية ؟ . كل هذا سوف نتعرف عليه في هذا المقال مدعوما بالصور.
المثلث قائم الزاوية حساب المساحة وطول أي ضلع
المثلث قائم الزاوية هو اقرب مثال لإيجاد مساحته وطول الضلع بسهولة تامة وهو ما يتعلمه طلبة المرحلة الابتدائية. اغلب الأمثلة التي تحتوي على حسابات المثلثات هي تلك التي تحتوي على قائم الزاوية وحتى المثلث غير قائم الزاوية يجري تحويله الى قائم من اجل سهولة الحساب.
مساحة المثلث قائم الزاوية = نصف القاعدة مضروبة في الارتفاع . لو افترضنا ان القاعدة هي B وهي اختصار Base والارتفاع هو H اختصار لكلمة Height سيكون القانون :
A=0.5* B*H
هذا يعني ان مساحة المثلث تساوي نصف مساحة مربع أو مستطيل وهذا القانون ينطبق على المثلثات قائمة الزاوية فقط دون غيرها.
معادلة الوتر للمثلث قائم الزاوية هي جذر مجموع مربعي القاعدة والارتفاع وسيكون القانون هو :
R=[(B^2+H^2)]^0.5
كما نعلم ان الرمز ^ يعني ان القوس او الضلع مرفوع الى اس يتم تحديد الرقم الخاص به . الاس 2 يعني تربيع بينما الاس 0.5 يعني نصف او جذر. يتم الحساب بهذه الطريقة للارقام المعروفة من خلال الحساب اليدوي وان كانت الارقام صعبة نلجأ الى الحاسبة اليدوية أو الالكترونية.
مثال على مثلث قائم الزاوية
في الامثلة على أي مثلث قائم الزاوية يتم اللجوء الى مثلث 3 , 4 , 5 لانه الاساس في اختبار او فحص ان كانت اي زاوية قائمة أم لا وذلك يتم القيام به عمليا. طريقة معرفة الزاوية ان كانت قائمة يتم قياس مسافة 3 او 30 سنتمتر من جهة ومن ثم قياس مسافة 4 او 40 سنتمتر من جهة اخرى. بعد تثبيت النقاط يتم قياس طول الوتر بواسطة شريط القياس او المسطرة فاذا كانت النتيجة 5 فهذا يعني ان الزاوية قائمة كما نشاهد في الصورة ادناه.

لو افترضنا ان طول الوتر اعلاه والذي طوله 5 متر غير معلوم نلجأ الى نظرية فيثاغورس لاستخراجه كما يلي :
R=[(3^2+4^2)]^0.5 = [9+16]^0.5 = [25]^0.5 = 5
تحقق لنا طول الوتر أعلاه فاثبتنا ان هذا الطول يمكن إيجاده بواسطة نظرية فيثاغورس والتي تنطبق فقط على المثلثات قائمة الزاوية ويمكن وضع أي ضلعين باي بعدين وإيجاد طول الوتر والتدرب عليعا كما في القانون والطريقة أعلاه.
لأيجاد مساحة المثلث اعلاه نطبق قانون المساحة كما ياتي :
A= 0.5 * 3*4 = 0.5 *12 = 6
المساحة تقاس بوحدة متر مربع او سنتيمتر مربع او اي وحدة طول اخرى مربعة.
إيجاد طول ضلع مثلث بمعلومية ضلع وزاويتين

لكي نجد طول ضلع مثلث بمعلومين ضلع وزاويتين فان قانون الجيب او Sine Law هو الحل والذي يكون عبارة عن خاصل قسمة طول الضلع على جيب الزاوية المقابلة يساوي طول الضبع الاخر على جيب الزاوية المقابلة وحسب القانون التالي : L1/Sine(1) = L2/Sine(2) = L3/Sine(3)
الاطوال اعلاه في القانون تم ترقيمها استنادا الى عدد اضلاع المثلث قلو شاهدنا المثلث اعلاه نجد ان هناك زاوية مفقودة ويمكن ايجاد هذه الزاوية استنادا الى مجموع زوايا المثلث التي تساوي 180 درجة بالتالي يكون لدينا القانون : Aangle (1) + Angle (2) + Angle (3) = 180 Degree
فتكون الزاوية المفقودة هي : 180- 50- 97 = 51 درجة
استخرجنا الزاوية المفقودة ونستطيع الآن أن نجد اطوال الاضلاع المفقودة استنادا الى معلومية ضلع بالإضافة الى الزاوية المقابلة له وكالاتي :
L1=(5.48)/Sine(51) = L2/Sine(79)
فيكو L2 = 6.92 وهو المقابل الى الزاوية 79 وبنفس الطريقة L3= 5.4 وهو المقابل الى الزاوية 50.
تعلمنا من خلال هذه الطريقة ايجاد اطوال الاضلاع لمثلث متوفرة فيه ضلع معلوم وزاويتين عن طريق قانون الجيب ولكن توجد طرق اخرى في ايجاد طول الضلع المفقود بالاضافة الى المسافة واهمية المحيط في استخراجها.
ايجاد طول ضلع مثلث بمعلومية زاوية وطولين معلومين
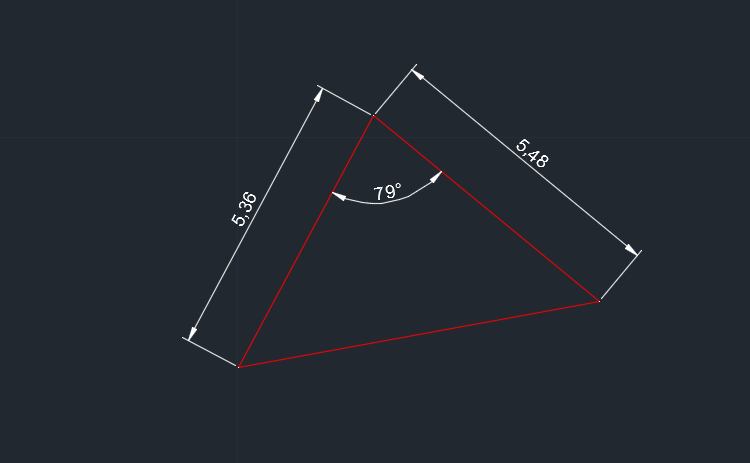
المثلث اعلاه يوجد فيه ضلعين معلومين وبينهما زاوية معروفة ونحتاج ايجاد الضلع الثالث. في هذه الحالة لا يمكن ان ينفعنا قانون فيثارغورس لانه يشترك ان تكون احدى زوايا المثلث قائمة. تعرفنا على اطوال الاضلاع لهذا المثلث اعلاه والتي تمت بواسطة قانون الجيب او Sine Law والان يجب ان نقوم بالتحقيق من خلال قانون الجيب تمام الذي يطبق في مثل هذه الحالة والذي يكون كما يلي:
L3 = [L1^2+L2^2 – 2 *L1* L2* Cos(3)]^0.5
طول الضلع المفقود يساوي مربع الضلع الاول زائدا مربع الضلع الثاني ناقصا ضعف ضرب الضلع الأول مع الثاني في جيب تمام الزاوية المقابلة. ناتج هذه العملية يتم جذرها للحصول على طول الضلع بواسطة قانون الجيب تمام أعلاه. نقوم بتطبيق مثال عملي ليكون الناتج هو : 6.92 وهو يحقق الرقم في الحالة أعلاه. هذا يعني ان حالات ايجاد طول الضلع سواء بواسطة قانون الجيب او الجيب تمام صحيحة ويمكن تحقيقها مع بعضها وإيجاد الزوايا بدمج هذين القانونين معا في ايجاد ما نريد في المثلثات غير قائمة الزاوية.
حساب مساحة مثلث غير قائم الزاوية
لحساب مساحة أي مثلث غير قائم الزاوية نقوم بحساب المحيط وهو طول اضلاعه الثلاثة والذي يكون كما يلي :
Perimeter = L1 +L2+L3
بعد حساب المحيط نفترض قيمة تسمى X والتي تكون قيمتها المحيط مفسوم على 2 أي :
X=Perimeter/2
قانون ايجاد مساحة المثلث غير قائم الزاوية هو جذر قيمة X ومضروبة في نفس القيمة ولكن ناقص كل ضلع من اضلاع المثلث والتي تكون كما يلي :
Area = [ X * (X-L1) * (X-L2) * (X-L3)]^0.5
بتطبيق هذا القانون سوف يظهر لنا ما يلي :
- المحيط للمثلث اعلاه = 17.8 ( تم اختيار طول الضلع 5.4 بدلا من الموجود في الصورة 5.36)
- قيمة X والتي تساوس المحيط مقسوم على 2 هي (8.9)
- تطبيق الثانون اعلاه سوف يظهر لنا مساحة قدرها (14.52)

نشاهد في الصورة اعلاه ان المساحة في الاوتوكاد تختلف بفارق اعشار عن المساحة المحسوبة وهناك اسباب كثيرة منها ان اوتوكاد دقته في الحساب الى غاية عشرين بينما استخدام الحاسبة الرياضية او الهندسية تعطي نتائج اكثر دقة.
تطبيق نفس المعادلة اعلاه على المثلث قائم الزاوية سوف تعطينا مساحة قدرها (6) يمكن تجربة العمل بهذا القانون واثبات اي ناتج او طول تريده. هذا يمكن ان يؤدس الى ايجاد اي مساحة تتكون من مثبثات في حالة معلومة زاوية وضلعين او زاويتين وضلع واحد وهي تفيد بشكل كبير على ارض الواقع.
إضافة تعليق
يجب عليك تسجيل الدخول او التسجيل لتستطيع اضافه تعليق .